ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ
ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ ਵਕਤ ਦੇ ਕਿਸੇ ਫੰਕਸ਼ਨ (ਕਿਸੇ ਸਿਗਨਲ) ਨੂੰ ਅਜਿਹੀਆਂ ਫਰੀਕੁਐਂਸੀਆਂ ਵਿੱਚ ਤੋੜ ਦਿੰਦਾ ਹੈ ਜੋ ਇਸਨੂੰ ਉਸੇ ਤਰੀਕੇ ਨਸਾਲ ਬਣਾ ਦਿੰਦੀਆਂ ਹਨ, ਜਿਵੇਂ ਕੋਈ ਸੰਗੀਤਕ ਤਾਰ ਨੂੰ ਇਸਦੇ ਰਚਣਹਾਰੇ ਨੋਟਾਂ ਦੇ ਐਂਪਲੀਟਿਊਡ (ਜਾਂ ਉੱਚੇਪਣ) ਦੇ ਤੌਰ 'ਤੇ ਦਰਸਾਇਆ ਜਾ ਸਕਦਾ ਹੈ।
-
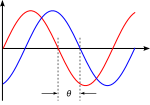
ਇੱਕ ਸਾਈਨੁਸੋਆਇਡਲ ਵਕਰ, ਜਿਸਦਾ ਉੱਚਤਮ ਐਂਪਲੀਟਿਊਡ (1) ਹੈ।
-
ਫੇਜ਼ ਸ਼ਿਫਟ θ ਦਾ ਚਿੱਤ੍ਰਣ।
| ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ |
|---|
| ਨਿਰੰਤਰ ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ |
| ਫੋਰੀਅਰ ਸੀਰੀਜ਼ |
| ਅਨਿਰੰਤਰ-ਸਮਾਂ ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ |
| ਅਨਿਰੰਤਰ ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ |
| ਕਿਸੇ ਛੱਲੇ ਉੱਪਰ ਅਨਿਰੰਤਰ ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ |
| ਫੋਰੀਅਰ ਵਿਸ਼ਲੇਸ਼ਣ |
| ਸਬੰਧਤ ਪਰਿਵਰਤਨ |
ਪਰਿਭਾਸ਼ਾ
ਸੋਧੋਇਤਿਹਾਸ
ਸੋਧੋਜਾਣ-ਪਛਾਣ
ਸੋਧੋਉਦਾਹਰਨ
ਸੋਧੋਫੋਰੀਅਰ ਪਰਿਵਰਤਨ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ
ਸੋਧੋਅਧਾਰ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ
ਸੋਧੋਉਲਟਾਤਮਿਕਤਾ ਅਤੇ ਆਵਰਤਾਮਿਕਤਾ
ਸੋਧੋਇਕਾਈਆਂ ਅਤੇ ਦੋਹਰਾਤਮਿਕਤਾ
ਸੋਧੋਇੱਕਸਾਰ ਨਿਰੰਤ੍ਰਤਾ ਅਤੇ ਰੀਮਾੱਨ-ਲੈਬਸਗਿਉ ਲੈੱਮਾ
ਸੋਧੋਪਲਾਚਿਰਿਲ ਥਿਊਰਮ ਅਤੇ ਪਾਰਸਵਲ ਦੀ ਥਿਊਰਮ
ਸੋਧੋਪੋਆਇਸ਼ਨ ਜੋੜ ਫਾਰਮੂਲਾ
ਸੋਧੋਡਿੱਫ੍ਰੈਂਟੀਏਸ਼ਨ
ਸੋਧੋਕਨਵੋਲਿਊਸ਼ਨ ਥਿਊਰਮ
ਸੋਧੋਆਰਪਾਰ-ਸਹਿਸਬੰਧ ਥਿਊਰਮ
ਸੋਧੋਆਈਗਬ-ਫੰਕਸ਼ਨ
ਸੋਧੋਹੇਜ਼ਨਬਰਗ ਗਰੁੱਪ ਨਾਲ ਸਬੰਧ
ਸੋਧੋਕੰਪਲੈਕਸ ਡੋਮੇਨ
ਸੋਧੋਲਾਪਲੇਸ ਪਰਿਵਰਤਨ
ਸੋਧੋਪਲਟੀ
ਸੋਧੋਯੁਕਿਲਡਨ ਸਪੇਸ ਉੱਤੇ ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ
ਸੋਧੋਅਨਸਰਟਨੀ ਸਿਧਾਂਤ
ਸੋਧੋਸਾਈਨ ਅਤੇ ਕੋਜ਼ਾਈਨ ਪਰਿਵਰਤਨ
ਸੋਧੋਗੋਲ ਹਾਰਮੋਨਿਕਾਂ
ਸੋਧੋਮਨਾਹੀ ਸਮੱਸਿਆਵਾਂ
ਸੋਧੋਫੰਕਸ਼ਨ ਸਪੇਸ ਉੱਤੇ ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ
ਸੋਧੋLp ਸਪੇਸਾਂ ਉੱਤੇ
ਸੋਧੋਛੇੜੀਆਂ ਹੋਈਆਂ ਵਿਸਥਾਰ-ਵੰਡਾਂ
ਸੋਧੋਸਰਵ-ਸਧਾਰੀਕਰਨਾਂ
ਸੋਧੋਫੋਰੀਅਰ-ਸਟਿਲਟਜਸ ਪਰਿਵਰਤਨ
ਸੋਧੋਸਥਾਨਿਕ ਤੌਰ 'ਤੇ ਸੁੰਗੜਿਆ ਅਬੇਲੀਅਨ ਗਰੁੱਪ
ਸੋਧੋਗਲਫਾਂਡ ਪਰਿਵਰਤਨ
ਸੋਧੋਸੁੰਗੜੇ ਗੈਰ-ਅਬੇਲੀਅਨ ਗਰੁੱਪ
ਸੋਧੋਬਦਲ
ਸੋਧੋਉਪਯੋਗ
ਸੋਧੋਡਿੱਫ੍ਰੈਂਸ਼ੀਅਲ ਇਕੁਏਸ਼ਨਾਂ ਦਾ ਵਿਸ਼ੇਲੇਸ਼ਣ
ਸੋਧੋਫੋਰੀਅਰ ਪਰਿਵਰਤਨ ਸਪੈਕਟ੍ਰੋਸਕੋਪੀ
ਸੋਧੋਕੁਆਂਟਮ ਮਕੈਨਿਕਸ
ਸੋਧੋਸੰਕੇਤ ਵਿਕਾਸ
ਸੋਧੋਹੋਰ ਧਾਰਨਾਵਾਂ
ਸੋਧੋਹੋਰ ਪ੍ਰੰਪ੍ਰਾਵਾਂ
ਸੋਧੋਹਿਸਾਬ ਵਿਧੀਆਂ
ਸੋਧੋਬੰਦ-ਅਕਾਰ ਫੰਕਸ਼ਨਾਂ ਦੀ ਸੰਖਿਅਨ ਇੰਟੀਗ੍ਰੇਸ਼ਨ
ਸੋਧੋਵਿਵਸਥਿਤ ਜੋੜਿਆਂ ਦੀ ਇੱਕ ਲੜੀ ਦੀ ਸੰਖਿਅਕ ਇੰਟੀਗ੍ਰੇਸ਼ਨ
ਸੋਧੋਅਨਿਰੰਤਰ ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ ਅਤੇ ਤੇਜ਼ ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ
ਸੋਧੋਮਹੱਤਵਪੂਰਨ ਫੋਰੀਅਰ ਪਰਿਵਰਤਨਾਂ ਦੀ ਸਾਰਣੀ
ਸੋਧੋਫੰਕਸ਼ਨਲ ਸਬੰਧਾਂ
ਸੋਧੋਵਰਗ-ਇੰਟੀਗ੍ਰੇਟਯੋਗ ਫੰਕਸ਼ਨ
ਸੋਧੋਵਿਸਥਾਰ-ਵੰਡਾਂ
ਸੋਧੋਦੋ-ਅਯਾਮੀ ਫੰਕਸ਼ਨ
ਸੋਧੋਸਰਵ-ਸਧਾਰਬ n-ਅਯਾਮੀ ਫੰਕਸ਼ਨਾਂ ਵਾਸਤੇ ਸੂਤਰ
ਸੋਧੋਇਹ ਵੀ ਦੇਖੋ
ਸੋਧੋ- ਐਨਾਲੌਗ ਸੰਕੇਤ ਵਿਕਾਸ
- ਬੀਵਰਜ਼-ਲਿਪਸਨ ਸਟਰਿਪ
- ਅਨਿਰੰਤਰ ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ
- ਅਨਿਰੰਤਰ-ਸਮਾਂ ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ
- ਤੇਜ਼ ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ
- ਫੋਰੀਅਰ ਇੰਟਗ੍ਰਲ ਓਪਰੇਟਰ
- ਫੋਰੀਅਰ ਇਨਵਰਸ਼ਨ ਥਿਓਰਮ
- ਫੋਰੀਅਰ ਮਲਟੀਪਲਾਇਰ
- ਫੋਰੀਅਰ ਸੀਰੀਜ਼
- ਫੋਰੀਅਰ ਸਾਈਨ ਪਰਿਵਰਤਨ
- ਫੋਰੀਅਰ-ਡੈਲੀਗਨੇ ਪਰਿਵਰਤਨ
- ਫੋਰੀਅਰ-ਮੁਕਾਇ ਪਰਿਵਰਤਨ
- ਭਿੰਨਾਤਮਿਕ ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ
- ਅਸਿੱਧਾ ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ
- ਇੰਟਗ੍ਰਲ ਪਰਿਵਰਤਨ
- ਲਾਪਲੇਸ ਪਰਿਵਰਤਨ
- ਰੇਖਿਕ ਕਾਨੋਨੀਕਲ ਪਰਿਵਰਤਨ
- ਮਿਲਿੱਨ ਪਰਿਵਰਤਨ
- ਬਹੁਅਯਾਮੀ ਪਰਿਵਰਤਨ
- NGC 4622, ਖਾਸਤੌਰ 'ਤੇ ਤਸਵੀਰ NGC 4622 ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ m = 2.
- ਅਲਪ-ਕਾਲੀਨ ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ
- ਸਪੇਸ-ਟਾਈਮ ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ
- ਸਪੈਕਟ੍ਰਲ ਘਣਤਾ
- ਚਿੰਨਾਤਮਿਕ ਇੰਟੀਗ੍ਰੇਸ਼ਨ
- ਸਮਾਂ ਖਿੱਚ ਡਿਸਪਰਸਿਵ ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ
- ਪਰਿਵਰਤਨ (ਗਣਿਤ)
ਟਿੱਪਣੀਆਂ
ਸੋਧੋਨੋਟਸ
ਸੋਧੋਹਵਾਲੇ
ਸੋਧੋ- Boashash, B., ed. (2003), Time-Frequency Signal Analysis and Processing: A Comprehensive Reference, Oxford: Elsevier Science, ISBN 0-08-044335-4
- Bochner S., Chandrasekharan K. (1949), Fourier Transforms, Princeton University Press
- Bracewell, R. N. (2000), The Fourier Transform and Its Applications (3rd ed.), Boston: McGraw-Hill, ISBN 0-07-116043-4.
- Campbell, George; Foster, Ronald (1948), Fourier Integrals for Practical Applications, New York: D. Van Nostrand Company, Inc..
- Condon, E. U. (1937), "Immersion of the Fourier transform in a continuous group of functional transformations", Proc. Natl. Acad. Sci. USA, 23: 158–164.
- Duoandikoetxea, Javier (2001), Fourier Analysis, American Mathematical Society, ISBN 0-8218-2172-5.
- Dym, H; McKean, H (1985), Fourier Series and Integrals, Academic Press, ISBN 978-0-12-226451-1.
- Erdélyi, Arthur, ed. (1954), Tables of Integral Transforms, vol. 1, New Your: McGraw-Hill
- Gerald Folland (1989), Harmonic analysis in phase space, Princeton University Press
- Fourier, J. B. Joseph (1822), Théorie Analytique de la Chaleur, Paris: Chez Firmin Didot, père et fils
- Fourier, J. B. Joseph; Freeman, Alexander, translator (1878), The Analytical Theory of Heat, The University Press
{{citation}}:|first2=has generic name (help)CS1 maint: multiple names: authors list (link) - Champeney, D.C. (1987), A Handbook of Fourier Theorems, Cambridge University Press
- de Groot, Sybren R.; Mazur, Peter (1984), Non-Equilibrium Thermodynamics (2nd ed.), New York: Dover
- Marín Antuña, José (1990), Teoría de funciones de variable compleja (2nd ed.), Havana: Editorial Pueblo y Educación
- Chatfield, Chris (2004), The Analysis of Time Series: An Introduction, Texts in Statistical Science (6th ed.), London: Chapman & Hall/CRC
- Feller, William (1971), An Introduction to Probability Theory and Its Applications. Vol. II. (Second ed.), New York: John Wiley & Sons, MR 0270403.
- Wiener, Norbert (1949), Extrapolation, Interpolation, and Smoothing of Stationary Time Series With Engineering Applications, Cambridge, Mass.: Technology Press and John Wiley & Sons and Chapman & Hall
- Kirillov, Alexandre; Gvichiani, Alexei (1982), Théorèmes et problèmes d'analyse fonctionnelle, Djilali Embarek, translator, Moscow: Mir
- Kolmogórov, Andréi Nikolaevich; Fomín, Serguei Vasílievich (1978), Elementos de la teoría de funciones y del análisis functional, Carlos Vega, translator (3rd ed.), Moscow: Mir
- Guelfand, Israel Moiseevich; Vilenkin, N.Y. (1967), Les distributions tome 4: applications de l'analyse harmonique, G. Rideau, translator, Paris: Dunod
- Widder, David Vernon; Wiener, Norbert (August 1938), "Remarks on the Classical Inversion Formula for the Laplace Integral", Bulletin of the American Mathematical Society, 44: 573–575, doi:10.1090/s0002-9904-1938-06812-7
- Clozel, Laurent; Delorme, Patrice (1985), "Sur le théorème de Paley-Wiener invariant pour les groupes de Lie réductifs réels", C. R. Acad. Sci. Paris, série I, 300: 331–333
- Paley, R.E.A.C.; Wiener, Norbert (1934), Fourier Transforms in the Complex Domain, American Mathematical Society Colloquium Publications, Providence, Rhode Island: American Mathematical Society
- Grafakos, Loukas (2004), Classical and Modern Fourier Analysis, Prentice-Hall, ISBN 0-13-035399-X.
- Grafakos, Loukas; Teschl, Gerald (2013), "On Fourier transforms of radial functions and distributions", J. Fourier Anal. Appl., 19: 167–179, doi:10.1007/s00041-012-9242-5.
- Greiner, W.; Reinhardt, J. (1996), Field Quantization, Springer Publishing, ISBN 3-540-59179-6
- Hewitt, Edwin; Ross, Kenneth A. (1970), Abstract harmonic analysis. Vol. II: Structure and analysis for compact groups. Analysis on locally compact Abelian groups, Die Grundlehren der mathematischen Wissenschaften, Band 152, Berlin, New York: Springer-Verlag, MR 0262773.
- Hörmander, L. (1976), Linear Partial Differential Operators, Volume 1, Springer-Verlag, ISBN 978-3-540-00662-6.
- James, J.F. (2011), A Student's Guide to Fourier Transforms (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-17683-5.
- Kaiser, Gerald (1994), A Friendly Guide to Wavelets, Birkhäuser, ISBN 0-8176-3711-7
- Kammler, David (2000), A First Course in Fourier Analysis, Prentice Hall, ISBN 0-13-578782-3
- Katznelson, Yitzhak (1976), An introduction to Harmonic Analysis, Dover, ISBN 0-486-63331-4
- Knapp, Anthony W. (2001), Representation Theory of Semisimple Groups: An Overview Based on Examples, Princeton University Press, ISBN 978-0-691-09089-4
- Müller, Meinard (2015), The Fourier Transform in a Nutshell. (PDF), In Fundamentals of Music Processing, Section 2.1, pages 40-56: Springer, doi:10.1007/978-3-319-21945-5, ISBN 978-3-319-21944-8, archived from the original (PDF) on 2016-04-08, retrieved 2016-06-26
{{citation}}: External link in|location= - Pinsky, Mark (2002), Introduction to Fourier Analysis and Wavelets, Brooks/Cole, ISBN 0-534-37660-6[permanent dead link]
- Polyanin, A. D.; Manzhirov, A. V. (1998), Handbook of Integral Equations, Boca Raton: CRC Press, ISBN 0-8493-2876-4.
- Rudin, Walter (1987), Real and Complex Analysis (Third ed.), Singapore: McGraw Hill, ISBN 0-07-100276-6.
- Rahman, Matiur (2011), Applications of Fourier Transforms to Generalized Functions, WIT Press, ISBN 1845645642.
- Stein, Elias; Shakarchi, Rami (2003), Fourier Analysis: An introduction, Princeton University Press, ISBN 0-691-11384-X.
- Stein, Elias; Weiss, Guido (1971), Introduction to Fourier Analysis on Euclidean Spaces, Princeton, N.J.: Princeton University Press, ISBN 978-0-691-08078-9.
- Taneja, HC (2008), "Chapter 18: Fourier integrals and Fourier transforms", Advanced Engineering Mathematics:, Volume 2, New Delhi, India: I. K. International Pvt Ltd, ISBN 8189866567.
- Titchmarsh, E (1948), Introduction to the theory of Fourier integrals (2nd ed.), Oxford University: Clarendon Press (published 1986), ISBN 978-0-8284-0324-5.
- Vretblad, Anders (2000), Fourier Analysis and its Applications, Graduate Texts in Mathematics, vol. 223, New York: Springer Publishing, ISBN 0-387-00836-5
- Wilson, R. G. (1995), Fourier Series and Optical Transform Techniques in Contemporary Optics, New York: Wiley, ISBN 0-471-30357-7.
- Yosida, K. (1968), Functional Analysis, Springer-Verlag, ISBN 3-540-58654-7.
ਬਾਹਰੀ ਲਿੰਕ
ਸੋਧੋ- Weisstein, Eric W., "ਫੋਰੀਅਰ ਪਰਿਵਰਤਨ" from MathWorld.