ਸਟਰਿੰਗ (ਭੌਤਿਕ ਵਿਗਿਆਨ)
ਕਿਸੇ ਬਿੰਦੂ ਵਰਗੇ ਕਣ ਦੀ ਗਤੀ ਦਰਸਾਉਣ ਲਈ ਇੱਕ ਗਰਾਫ ਤੇ ਇਸ ਦਾ ਸਥਾਨ ਵਕਤ ਦੇ ਹਿਸਾਬ ਨਾਲ ਦਰਸਾਇਆ ਜਾ ਸਕਦਾ ਹੈ। ਨਤੀਜਨ ਤਸਵੀਰ ਸਪੇਸ ਸਮੇਂ ਵਿੱਚ ਉਸਦ ਕਣ ਦੀ ਸੰਸਾਰ-ਰੇਖਾ ਦਰਸਾਏਗੀ| ਇੱਕ ਹੋਰ ਬਰਾਬਰ ਤਰੀਕੇ ਨਾਲ, ਵਕਤ ਦੇ ਗੁਜ਼ਰਨ ਦੇ ਨਾਲ ਨਾਲ ਸਟਰਿੰਗ ਦੀ ਗਤੀ ਨੂੰ ਦਰਸਾਇਆ ਜਾ ਸਕਦਾ ਹੈ। ਸਟਰਿੰਗ, ਜੋ ਆਪਣੇ ਆਪ ਵਿੱਚ ਛੋਟੀ ਰੇਖਾ ਵਾਂਗ ਦਿਸਦੇ ਹਨ, ਇੱਕ 2-ਪਸਾਰੀ ਸਤਿਹ ਝਾੜਦੇ ਜਾਂਦੇ ਹਨ ਜਿਸ ਨੂੰ ਵਰਲਡਸ਼ੀਟ (ਸੰਸਾਰੀ ਚਾਦਰ) ਕਹਿੰਦੇ ਹਨ। ਵੱਖਰੀਆਂ ਸਟਰਿੰਗ ਹਾਲਤਾਂ (ਫੋਟੋਨ ਜਾਂ ਗਰੈਵੀਟੋਨ ਵਰਗੇ ਵੱਖਰੇ ਕਣਾਂ ਨੂੰ ਰਚਦੇ ਹੋਏ) ਇਸ ਸਤਹਿ ਤੇ ਤਰੰਗਾਂ ਵਾਂਗ ਲਗਦੇ ਹਨ।
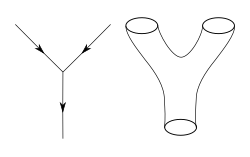
ਇੱਕ ਬੰਦ ਸਟਰਿੰਗ ਇੱਕ ਛੋਟੇ ਲੂਪ ਵਾਂਗ ਦਿਸਦਾ ਹੈ, ਇਸਲਈ ਇਸ ਦੀ ਵਰਲਡਸ਼ੀਟ ਪਾਈਪ ਵਾਂਗ ਦਿਸੇਗੀ| ਇੱਕ ਖੁੱਲਾ ਸਟਰਿੰਗ ਦੋ ਸਿਰਿਆਂ ਵਾਲੇ ਛੋਟੇ ਹਿੱਸੇ ਵਾਂਗ ਦਿਸੇਗਾ, ਇਸਲਈ ਇਸ ਦੀ ਵਰਲਡਸ਼ੀਟ ਇੱਕ ਪੱਟੀ ਵਰਗੀ ਦਿਸੇਗੀ| ਹੋਰ ਜਿਆਦਾ ਗਣਿਤੀ ਭਾਸ਼ਾ ਵਰਤਦੇ ਹੋਏ, ਇਹ ਦੋਵੇਂ ਰਾਈਮਨ ਤਲ (Riemann surfaces) ਹਨ, ਜਿਸ ਵਿੱਚ ਪੱਟੀ ਦੀ ਇੱਕ ਹੱਦ ਹੁੰਦੀ ਹੈ ਪਰ ਪਾਈਪ ਦੀ ਹੱਦ ਨਹੀਂ ਹੁੰਦੀ|
ਸਟਰਿੰਗ ਜੁੜ ਅਤੇ ਟੁੱਟ ਸਕਦੇ ਹਨ। ਇਹ ਉਹਨਾਂ ਦੀ ਵਰਡਲਸ਼ੀਟ ਤੋਂ ਪਤਾ ਚਲਦਾ ਹੈ, ਜਾਂ ਸੰਖੇਪ ਵਿੱਚ ਕਹੀਏ ਤਾਂ ਉਹਨਾਂ ਦੇ ਸਮਸਥਿਤੀ (topology) ਤੋਂ ਪਤਾ ਚਲਦਾ ਹੈ। ਜਿਵੇਂ, ਜੇ ਇੱਕ ਬੰਦ ਸਟਰਿੰਗ ਟੁੱਟਦਾ ਹੈ, ਤਾਂ ਇਸ ਦੀ ਸੰਸਾਰਸ਼ੀਟ ਇੱਕ ਪਾਈਪ ਦੋ ਪਾਈਪਾਂ ਵਿੱਚ ਤਬਦੀਲ ਹੋਣ ਵਾਂਗ ਗੁਲੇਲ ਵਾਂਗ ਦਿਸਦਾ ਹੈ। ਇਹ ਸਮਸਥਾਨ ਪੈਂਟਾਂ ਦੇ ਜੋੜੇ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਜੇ ਇੱਕ ਬੰਦ ਰਿੰਗ ਟੁੱਟਦਾ ਹੈ ਅਤੇ ਇਸ ਦੇ ਦੋ ਹਿੱਸੇ ਦੁਬਾਰਾ ਜੁੜਦੇ ਹਨ, ਫੇਰ ਇਸ ਦੀ ਸੰਸਾਰਸ਼ੀਟ ਇੱਕ ਪਾਈਪ ਦੀ ਤਰਾਂ ਬਣਦੀ ਹੈ ਜੋ ਪਹਿਲਾਂ ਖੁੱਲੇ ਸਿਰੇ ਵਾਲਾ ਹੁੰਦਾ ਹੈ ਫੇਰ ਜੁੜ ਕੇ ਦੁਬਾਰਾ ਉਹੀ ਰਿੰਗ ਬਣ ਜਾਂਦਾ ਹੈ, ਪਰ ਇੱਕ ਹੋਰ ਤਰਾਂ ਦਾ ਰਿੰਗ ਵੀ ਬਣ ਸਕਦਾ ਹੈ ਜੋ ਫੁੱਲ ਵਾਂਗ ਅੱਧਾ ਚੱਕਰ ਹਾਸ਼ੀਏ (torus) ਵਾਂਗ ਦਿਸ ਸਕਦਾ ਹੈ ਜੋ ਦੋ ਪਾਈਪਾਂ ਨੂੰ ਜੁੜਿਆ ਹੁੰਦਾ ਹੈ (ਇੱਕ ਆਉਣ ਵਾਲਾ ਸਟਰਿੰਗ, ਅਤੇ ਦੂਜਾ ਜਾਣ ਵਾਲਾ ਸਟਰਿੰਗ ਦਰਸਾਉਂਦਾ ਹੈ)| ਇੱਕ ਖੁੱਲਾ ਸਟਰਿੰਗ ਜੋ ਅਜਿਹਾ ਹੀ ਕਰ ਰਿਹਾ ਹੋਵੇ ਉਸ ਦੀ ਵਰਲਡਸ਼ੀਟ ਇੰਝ ਦਿਸ ਸਕਦੀ ਹੈ ਜਿਵੇਂ ਅੰਗੂਠੀ(annulus) ਦੋ ਪੱਟੀਆਂ ਨਾਲ ਜੁੜੀ ਹੁੰਦੀ ਹੈ।
ਕੁਆਂਟਮ ਮਕੈਨਿਕਸ ਵਿੱਚ, ਇੱਕ ਕਣ ਦੀ ਉਦ ਸੰਭਾਵਨਾ ਗਿਣੀ ਜਾਂਦੀ ਹੈ ਜਿਸ ਨਾਲ ਉਹ ਇੱਕ ਬਿੰਦੂ ਤੋਂ ਦੂਜੇ ਬਿੰਦੂ ਤੱਕ ਕੁੱਝ ਨਿਸ਼ਚਿਤ ਮੁੱਲਾਂ ਨੂੰ ਜੋੜ ਕੇ ਲੰਘ ਸਕਦਾ ਹੋਵੇ, ਜਿਨਾਂ ਨੂੰ ਸੰਭਾਵ ਅਯਾਮ (probability amplitudes) ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਹਰੇਕ ਅਯਾਮ ਇੱਕ ਕਣ ਦੀ ਸੰਸਾਰ ਰੇਖਾ ਨਾਲ ਜੁੜਿਆ ਹੁੰਦਾ ਹੈ। ਸਾਰੀਆਂ ਸੰਭਵ ਸੰਸਾਰ ਰੇਖਾਵਾਂ ਦੇ ਅਯਾਮਾਂ ਦੇ ਜੋੜ ਦੀ ਇਹ ਵਿਧੀ ਰਸਤਾ ਏਕੀਕਰਨ (path integration) ਕਹਾਉਂਦੀ ਹੈ। ਸਟਰਿੰਗ ਥਿਊਰੀ ਵਿੱਚ, ਇੱਕ ਸ਼ੁਰੂਆਤੀ ਸਟਰਿੰਗ ਬਣਤਰ ਤੋਂ ਅੰਤਮ ਸਟਰਿੰਗ ਬਣਤਰ ਤੱਕ ਦੀਆਂ ਸੰਸਾਰਸ਼ੀਟਾਂ ਨਾਲ ਸਬੰਧਤ ਸੰਖਿਆਵਾਂ ਨਾਲ, ਇਸੇ ਤਰਾਂ ਸੰਭਾਵਨਾਵਾਂ ਦਾ ਹਿਸਾਬ ਲਗਦਾ ਹੈ। ਇਹ ਗੱਲ ਸਮਝ ਵਿੱਚ ਹੈ ਕਿ ਸਟਰਿੰਗ ਥਿਊਰੀ ਕੁਆਂਟਮ ਫੀਲਡ ਥਿਊਰੀ ਨੂੰ ਬਿੰਦੂ-ਕਣਾਂ ਦੇ ਸਟਰਿੰਗਾਂ ਵਿੱਚ ਬਦਲਣ ਕਾਰਨ ਹੋਰ ਵਧਾਉਂਦੀ ਹੈ। ਜਿਵੇਂ ਕੁਆਂਟਮ ਫੀਲਡ ਥਿਊਰੀ ਵਿੱਚ, ਫੀਲਡਾਂ ਦੇ ਪੁਰਾਣੇ ਤਰੀਕੇ ਵਿੱਚ ਕਾਰਜ ਦੇ ਫੰਕਸ਼ਨ ਰਾਹੀਂ ਖੇਤਰ ਨਿਰਧਾਰਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਉਵੇਂ ਹੀ ਇਹ ਸਟਰਿੰਗ ਥਿਊਰੀ ਵਿੱਚ ਜਾਂ ਨੰਬੂ-ਗੋਟੋ ਕਾਰਜ ਹੋ ਸਕਦਾ ਹੈ ਜਾਂ ਪੌਲੀਜੋਵ ਕਾਰਜ (Nambu-Goto action or Polyakov action) ਹੋ ਸਕਦਾ ਹੈ।
ਇਹ ਵੀ ਦੇਖੋ
ਸੋਧੋਹਵਾਲੇ
ਸੋਧੋ- Schwarz, John (2000). "Introduction to Superstring Theory" Archived 2019-07-08 at the Wayback Machine.. Retrieved Dec. 12, 2005.
- "NOVA's strings homepage"