ਗੈਲੀਲੀਅਨ ਟ੍ਰਾਂਸਫੋਰਮੇਸ਼ਨ

ਭੌਤਿਕ ਵਿਗਿਆਨ ਅੰਦਰ ਇੱਕ ਗੈਲੀਲੀਅਨ ਟ੍ਰਾਂਸਫੋਰਮੇਸ਼ਨ ਦੋ ਅਜਿਹੀਆਂ ਰੈਫ੍ਰੈਂਸ ਫ੍ਰੇਮਾਂ ਦੇ ਨਿਰਦੇਸ਼ਾਂਕਾਂ (ਕੋਆਰਡੀਨੇਟਾਂ) ਦਰਮਿਆਨ ਰੂਪਾਂਤ੍ਰਨ ਕਰਨ ਵਾਸਤੇ ਵਰਤੀ ਜਾਂਦੀ ਹੈ, ਜੋ ਨਿਊਟੋਨੀਅਨ ਭੌਤਿਕ ਵਿਗਿਆਨ ਦੀਆਂ ਬਣਤਰਾਂ ਅੰਦਰ ਸਿਰਫ ਸਥਿਰ ਸਾਪੇਖਿਕ (ਰੀਲੇਟੀਵਿਸਟਿਕ) ਗਤੀ ਦਾ ਹੀ ਫਰਕ ਰੱਖਦੀਆਂ ਹਨ।

ਇੱਕ ਬੁਨਿਆਦੀ ਮੰਤਵ, ਸਾਪੇਖਿਕ ਗਤੀ ਵਿੱਚ ਔਬਜ਼ਰਵਰਾਂ ਦੁਆਰਾ ਲਏ ਗਏ ਨਾਪਾਂ ਦੀ ਤੁਲਨਾ ਕਰਨ ਦੇ ਯੋਗ ਹੋਣਾ ਹੈ। ਮੰਨ ਲਓ ਸਾਡੇ ਕੋਲ ਫ੍ਰੇਮ S ਵਿੱਚ ਔਬਜ਼ਰਵਰ O ਹੈ ਜੋ ਕਿਸੇ ਘਟਨਾ ਨੂੰ ਤਿੰਨ ਕਾਰਟੀਜ਼ੀਅਨ ਨਿਰਦੇਸ਼ਾਂਕ ਅਤੇ ਉਸਦੇ ਮੇਲ ਕੀਤੇ ਹੋਏ ਕਲੌਕਾਂ (x, y, z, t) (ਦੇਖੋ ਚਿੱਤਰ. 1‑1) ਦੇ ਜਾਲ ਉੱਤੇ ਨਾਪਿਆ ਗਿਆ ਵਕਤ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ। ਇੱਕ ਵੱਖਰੀ ਫ੍ਰੇਮ S’ ਅੰਦਰਲਾ ਇੱਕ ਦੂਜਾ ਔਬਜ਼ਰਵਰ ਉਸਦੇ “ਕੋ-ਆਰਡੀਨੇਟ ਸਿਸਟਮ” ਵਿੱਚ ਓਸੇ ਘਟਨਾ ਅਤੇ ਮੇਲ ਕੀਤੇ ਹੋਏ (', ', ', ') ਕਲੌਕਾਂ ਦੇ ਜਾਲ ਨੂੰ ਨਾਪਦਾ ਹੈ। ਕਿਉਂਕਿ ਅਸੀਂ ਇਨ੍ਰਸ਼ੀਅਲ ਫ੍ਰੇਮਾਂ ਨਾਲ ਵਰਤ ਰਹੇ ਹੁੰਦੇ ਹਾਂ, ਇਸਲਈ ਕੋਈ ਵੀ ਔਬਜ਼ਰਵਰ ਪ੍ਰਵੇਗ (ਐਕਸਲ੍ਰੇਸ਼ਨ) ਅਧੀਨ ਨਹੀਂ ਹੁੰਦਾ ਹੈ, ਅਤੇ ਸਮੀਕਰਨਾਂ ਦਾ ਇੱਕ ਸਰਲ ਸੈੱਟ ਸਾਨੂੰ ਨਿਰਦੇਸ਼ਾਂਕਾਂ (x, y, z, t) ਨੂ੍ੰ ਨਿਰਦੇਸ਼ਾਂਕਾਂ (', ', ', ') ਨਾਲ ਸਬੰਧਤ ਕਰਨ ਦੀ ਆਗਿਆ ਦਿੰਦਾ ਹੈ। ਇਹ ਦਿੱਤਾ ਹੋਣ ਤੇ ਕਿ ਦੋ “ਕੋ-ਆਰਡੀਨੇਟ ਸਿਸਟਮ” ਮਿਆਰੀ ਰਚਨਾ ਵਿੱਚ ਹਨ, ਇਹ ਅਰਥ ਨਿਕਲਦਾ ਹੈ ਕਿ ਇਹ (x, y, z) ਨਿਰਦੇਸ਼ਾਂਕਾਂ ਨਾਲ ਸਮਾਂਤਰ ਰੱਖੇ ਹੁੰਦੇ ਹਨ ਅਤੇ t = 0 ਹੁੰਦਾ ਹੈ ਜਦੋਂ ' = 0 ਹੋਵੇ, ਤਾਂ ਨਿਰਦੇਸ਼ਾਂਕ ਰੂਪਾਂਤ੍ਰਨ ਇਸ ਤਰਾਂ ਹੁੰਦਾ ਹੈ:

$x'=x-vt$

$y'=y$

$z'=z$

$t'=t.$

ਚਿੱਤਰ 3-1. ਗੈਲੀਲੀਅਨ ਸਪੇਸਟਾਈਮ ਅਤੇ ਵਿਲੌਸਟੀਆਂ ਦੀ ਕੰਪੋਜ਼ੀਸ਼ਨ

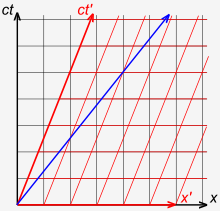
ਚਿੱਤਰ. 3-1 ਸਮਝਾਉਂਦਾ ਹੈ ਕਿ ਨਿਊਟਨ ਦੀ ਥਿਊਰੀ ਅੰਦਰ, ਸਮਾਂ ਯੂਨੀਵਰਸਲ (ਸੰਸਾਰੀ) ਹੁੰਦਾ ਹੈ, ਨਾ ਕਿ ਪ੍ਰਕਾਸ਼ ਦੀ ਵਿਲੌਸਟੀ। ਅੱਗੇ ਲਿਖਿਆ ਸੋਚ ਪ੍ਰਯੋਗ ਵਿਚਾਰੋ: ਲਾਲ ਤੀਰ ਪਲੇਟਫਾਰਮ ਦੇ ਸੰਦ੍ਰਭ ਵਿੱਚ 0.4 c ਉੱਤੇ ਗਤੀਸ਼ੀਲ ਕੋਈ ਰੇਲਗੱਡੀ ਦਿਖਾਉਂਦਾ ਹੈ। ਰੇਲਗੱਡੀ ਅੰਦਰ, ਕੋਈ ਯਾਤਰੀ ਗੋਲੀ ਸ਼ੂਟ ਕਰਦਾ ਹੈ ਜੋ ਰੇਲਗੱਡੀ ਦੀ ਫ੍ਰੇਮ ਅੰਦਰ 0.4 c ਦੀ ਸਪੀਡ ਵਾਲੀ ਹੁੰਦੀ ਹੈ। ਨੀਲ ਤੀਰ ਸਮਝਾਉਂਦਾ ਹੈ ਕਿ ਰੇਲਗੱਡੀ ਦੀ ਪਟੜੀ ਉੱਤੇ ਖੜਾ ਕੋਈ ਇਨਸਾਨ ਗੋਲੀ ਦੀ ਸਪੀਡ ਨੂੰ 0.8 c ਨਾਪਦਾ ਹੈ। ਇਹ ਸਾਡੀਆਂ ਮੂਲ ਉਮੀਦਾਂ ਅਨੁਸਾਰ ਹੀ ਹੈ।

ਹੋਰ ਸਰਵ ਸਧਾਰਨ ਤੌਰ ਤੇ, ਮੰਨ ਲਓ ਫ੍ਰੇਮ S ਦੇ ਸੰਦ੍ਰਭ ਵਿੱਚ ਫ੍ਰੇਮ S’ ਵਿਲੌਸਿਟੀ v ਨਾਲ ਗਤੀ ਕਰ ਰਹੀ ਹੈ। ਫ੍ਰੇਮ S’ ਅੰਦਰ, ਔਬਜ਼ਰਵਰ O’ ਕਿਸੇ ਚੀਜ਼ ਨੂੰ ਵਿਲੌਸਿਟੀ ' ਨਾਲ ਗਤੀਸ਼ੀਲ ਹੁੰਦੀ ਨਾਪਦਾ ਹੈ। ਫ੍ਰੇਮ S ਦੇ ਸੰਦ੍ਰਭ ਵਿੱਚ ਇਸਦੀ ਵਿਲੌਸਿਟੀ u ਕੀ ਹੁੰਦੀ ਹੈ? ਕਿਉਂਕਿ x = ut, ' = x − vt, ਅਤੇ t = ' ਹੁੰਦਾ ਹੈ, ਇਸਲਈ ਅਸੀਂ ' = ut − vt = (u − v)t = (u − v)' ਲਿਖ ਸਕਦੇ ਹਾਂ। ਇਹ ' = '/' ਵੱਲ ਲਿਜਾਂਦਾ ਹੈ ਅਤੇ ਅੰਤ ਨੂੰ

$u'=u-v$  or  $u=u'+v,$

ਜੋ ਸਾਂਝੀ-ਸਮਝ ਵਿਲੌਸਟੀਆਂ ਦੇ ਜੋੜ ਵਾਸਤੇ ਗੈਲੀਲੀਅਨ ਨਿਯਮ ਹੈ।

ਹਵਾਲੇ

• Arnold, V. I. (1989). Mathematical Methods of Classical Mechanics (2 ed.). Springer-Verlag. p. 6. ISBN 0-387-96890-3. {{cite book}}: Invalid |ref=harv (help)
• Bargmann, V. (1954). "On Unitary Ray Representations of Continuous Groups". Annals of Mathematics. 2. 59 (1): 1–46. doi:10.2307/1969831. {{cite journal}}: Invalid |ref=harv (help)
• Copernicus, Nicolaus; Kepler, Johannes; Galalei, Galileo; Newton, Isaac; Einstein, Albert (2002). Hawking, Stephen (ed.). On the Shoulders of Giants: The Great Works of Physics and Astronomy. Philadelphia, London: Running Press. pp. 515–520. ISBN 0-7624-1348-4. {{cite book}}: Unknown parameter |editorlink= ignored (|editor-link= suggested) (help)
• Galilei, Galileo (1638I). Discorsi e Dimostrazioni Matematiche, intorno á due nuoue scienze (in Italian). Leiden: Elsevier. pp. 191–196. {{cite book}}: Invalid |ref=harv (help)CS1 maint: unrecognized language (link)
• Galileo, Galilei (1638E). Discourses and Mathematical Demonstrations Relating to Two New Sciences [Discorsi e Dimostrazioni Matematiche Intorno a Due Nuove Scienze]. Translated to English 1914 by Henry Crew and Alfonso de Salvio. {{cite book}}: Invalid |ref=harv (help)
• Gilmore, Robert (2006). Lie Groups, Lie Algebras, and Some of Their Applications. Dover Books on Mathematics. Dover Publications. ISBN 0486445291. {{cite book}}: Invalid |ref=harv (help)
• Hoffmann, Banesh (1983), Relativity and Its Roots, Scientific American Books, ISBN 0-486-40676-8, Chapter 5, p. 83
• Lerner, Lawrence S. (1996), Physics for Scientists and Engineers, vol. 2, Jones and Bertlett Publishers, Inc, ISBN 0-7637-0460-1, Chapter 38 §38.2, p. 1046,1047
• Mould, Richard A. (2002), Basic relativity, Springer-Verlag, ISBN 0-387-95210-1, Chapter 2 §2.6, p. 42
• Nadjafikhah, Mehdi; Forough, Ahmad-Reza (2009). "Galilean Geometry of Motions" (PDF). Applied Sciences. pp. 91–105.
• Serway, Raymond A.; Jewett, John W. (2006), Principles of Physics: A Calculus-based Text (4th ed.), Brooks/Cole - Thomson Learning, ISBN 0-534-49143-X, Chapter 9 §9.1, p. 261