ਫ਼ੀਬੋਨਾਚੀ ਤਰਤੀਬ

ਹਿਸਾਬ ਵਿੱਚ ਫ਼ੀਬੋਨਾਚੀ ਹਿੰਦਸੇ ਜਾਂ ਫ਼ੀਬੋਨਾਚੀ ਤਰਤੀਬ/ਸਿਲਸਿਲਾ ਗਿਣਤੀ ਦੇ ਉਹਨਾਂ ਅੰਕਾਂ ਨੂੰ ਆਖਿਆ ਜਾਂਦਾ ਹੈ ਜੋ ਪੂਰਨ ਰਾਸ਼ੀਆਂ ਦੀ ਹੇਠ ਲਿਖੀ ਤਰਤੀਬ ਵਿੱਚ ਬੰਨ੍ਹੇ ਹੋਣ:

ਸਿਲਸਿਲੇਵਾਰ ਫ਼ੀਬੋਨਾਚੀ ਅੰਕਾਂ ਜਿੰਨੀ ਲੰਬਾਈ ਵਾਲ਼ੀਆਂ ਬਾਹੀਆਂ ਵਾਲ਼ੇ ਵਰਗਾਂ ਨਾਲ਼ ਬਣੀ ਇੱਕ ਟੈਲ

$1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\;\ldots \;$

ਜਾਂ (ਅਕਸਰ ਅਜੋਕੀ ਵਰਤੋਂ ਵਿੱਚ):

$0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\;\ldots \;$ (ਓਈਆਈਐੱਸ ਵਿੱਚ ਤਰਤੀਬ A000045).

ਫ਼ੀਬੋਨਾਚੀ ਚੂੜੀਦਾਰ: ਸੁਨਹਿਰੀ ਚੂੜੀਦਾਰ ਦਾ ਅੰਦਾਜ਼ਾ ਜੋ ਫ਼ੀਬੋਨਾਚੀ ਟੈਲ ਵਿਚਲੇ ਵਰਗਾਂ ਦੇ ਉਲਟੇ ਕੋਨਿਆਂ ਨੂੰ ਜੋੜਦੇ ਹੋਏ ਚੱਕਰਦਾਰ ਕੌਸ ਬਣਾ ਕੇ ਸਿਰਜਿਆ ਜਾਂਦਾ ਹੈ; ਇਹ ਵਾਲ਼ੇ ਵਿੱਚ 1, 1, 2, 3, 5, 8, 13, 21 ਅਤੇ 34 ਅਕਾਰ ਦੀਆਂ ਬਾਹੀਆਂ ਵਾਲ਼ੇ ਵਰਗ ਵਰਤੇ ਗਏ ਹਨ।

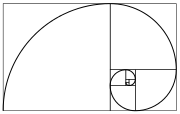
ਪਰਿਭਾਸ਼ਾ ਮੁਤਾਬਕ ਫ਼ੀਬੋਨਾਚੀ ਤਰਤੀਬ ਦੇ ਪਹਿਲੇ ਦੋ ਅੰਕ ਤਰਤੀਬ ਦੇ ਚੁਣੇ ਗਏ ਸ਼ੁਰੂਆਤੀ ਬਿੰਦੂ ਮੁਤਾਬਕ ਜਾਂ 1 ਅਤੇ 1 ਹੁੰਦੇ ਹਨ ਜਾਂ ਫੇਰ 0 ਅਤੇ 1 ਅਤੇ ਇਹਨਾਂ ਤੋਂ ਅਗਲੇ ਸਾਰੇ ਅੰਕ ਆਪਣੇ ਪਿਛਲੇ ਦੋ ਅੰਕਾਂ ਦਾ ਜੋੜ ਹੁੰਦੇ ਹਨ।

ਹਿਸਾਬੀ ਭਾਸ਼ਾ ਵਿੱਚ ਫ਼ੀਬੋਨਾਚੀ ਹਿੰਦਸਿਆਂ ਦੀ ਤਰਤੀਬ F_n ਨੂੰ ਇਹ ਮੁੜ-ਵਾਪਰਦਾ ਬਿਆਨ ਦਰਸਾਉਂਦਾ ਹੈ

$F_{n}=F_{n-1}+F_{n-2},\!\,$

ਜਿਹਦੇ ਮੁਢਲੇ ਮੁੱਲ

$F_{1}=1,\;F_{2}=1$

or

$F_{0}=0,\;F_{1}=1$

ਹੁੰਦੇ ਹਨ।

ਬਾਹਰਲੇ ਜੋੜ

• Periods of Fibonacci Sequences Mod m at MathPages
• Scientists find clues to the formation of Fibonacci spirals in nature
• Hrant Arakelian. Mathematics and History of the Golden Section, Logos 2014, 404 p. ISBN 978-5-98704-663-0 (rus.)
• Fibonacci Sequence on In Our Time at the BBC. (listen now)
• Hazewinkel, Michiel, ed. (2001), "Fibonacci numbers", ਗਣਿਤ ਦਾ ਵਿਸ਼ਵਕੋਸ਼, ਸਪਰਿੰਗਰ, ISBN 978-1-55608-010-4
• "Sloane's A000045 : Fibonacci Numbers", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.